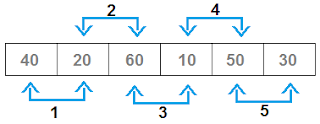
- In Bubble sort, each pair of adjacent items are compared and swapped if they are in the wrong order, as shown below.
- Bubble sort iterates through a array, compares adjacent items and swap them if they are out of order. In each iteration, Largest item will be moved(bubble up) at its proper place.
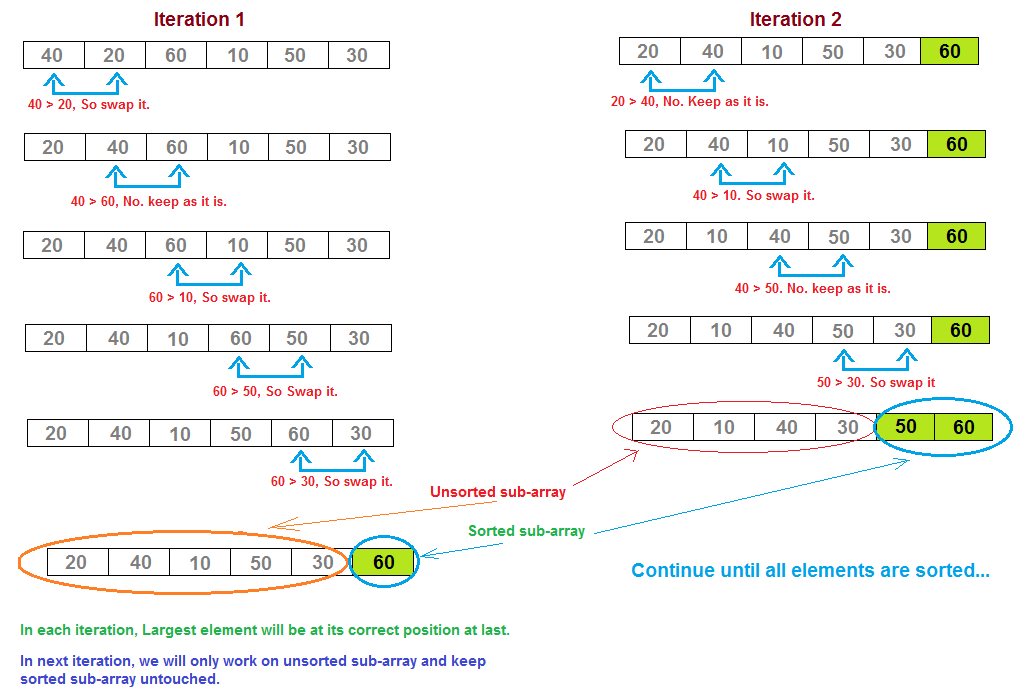
- So in above example, initially 40 and 20 will be compared. 40 > 20? Yes.
So 40 and 20 will be swapped.
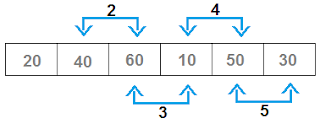
- Now, 40 and 60 will be compared, 40 > 60? No. So no need to swap and go ahead.
- Now, 60 and 10 will be compared, 60 > 10? Yes. So 60 and 10 will be swapped.
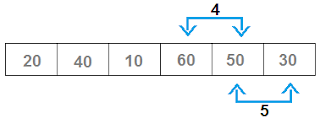
- Now, 60 and 50 will be compared, 60 > 50? Yes. So 60 and 50 will be swapped.
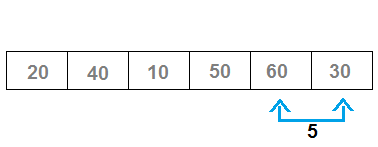
- Now, 60 and 30 will be compared, 60 > 30? Yes. So 60 and 30 will be swapped and largest item 60 bubbled up at its proper place.
- Repeat the steps for remaining unsorted sub-array and each iteration through the array places the next largest value in its proper place.
public class BubbleSort {
public static void main(String[] args) {
new BubbleSort();
}
public BubbleSort() {
int[] arr = new int[] { 2, 5, 3, 1, 4, 5, 1 };
System.out.println("Before Sorting...");
printArray(arr);
bubbleSort(arr);
System.out.println("\nAfter Sorting...");
printArray(arr);
}
private void bubbleSort(int[] arr) {
if (arr == null)
return;
boolean isSorted = true;
for (int i = 0; i < arr.length - 1; i++) {
for (int j = 1; j < arr.length - i; j++) {
if (arr[j - 1] > arr[j]) {
isSorted = false;
int temp = arr[j];
arr[j] = arr[j - 1];
arr[j - 1] = temp;
}
}
// Remember that a bubble sort will continue until no swaps have
// occurred,
// which says that array is in proper sorted order.
if (isSorted) {
break;
}
}
}
private void printArray(int arr[]) {
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
}
}
Complexity
- Time complexity of Bubble sort in Worst Case is O(N^2), which makes it quite inefficient for sorting large data volumes.
- O(N^2) because it sorts only one item in each iteration and in each iteration it has to compare n-i
elements. - Time complexity of Bubble sort in BestCase is O(N).
- When the given data set is already sorted, in that case bubble sort can identify it in one single iteration hence O(N).
- It means while iteratng, from i=0 till arr.length, if there is no swapping required, then the array is already sorted and stop there.
- Bubble sort can identify when the list is sorted and can stop early.
- Bubble sort is efficient for (quite) small data sets.
- It takes O(1) extra space.