“How will you calculate complexity of algorithm” is very common question in interview.How will you compare two algorithm? How running time get affected when input size is quite large? So these are some question which is frequently asked in interview.In this post,We will have basic introduction on complexity of algorithm and also to big o notation
- You need to evaluate an algorithm so that you can find most optimize algorithm for solving any problem.
- For example: You want to go from city A to City B.Then there are various choices available i.e. by flight,bus or train.So you need to choose among different options depending on your budget and urgency.
Counting number of instructions:
- Number of instructions can be different for different programming languages.
- Lets count number of instruction for searching a element in a array.
int n=array.length
for (int i = 0; i < n; i++) {
if(array[i]==elementToBeSearched)
return true;
}
return false;
}
- Let’s assume our processor takes one instruction for each of the operation:
- For assigning a value to a variable.
- For comparing two values.
- Multiply or addition.
- Return statement
- In Worst case:
- If element which we want to search is last element in sorted array then it will be worst case here.
if(array[i]==elementToBeSearched), i++ and i<n
will be executed n times
int n=array.length, i=0, return true or false
will be executed 1 time
Hence f(n)=3n+3
Asymptotic behaviour:
Here We will see how f(n) performs with larger value of n.Now in above function, we have two parts i.e. 3n and 3. Here you can note two points:
- As n grows larger, we can ignore constant 3 as it will be always 3 irrespective of value of n. It makes sense as you can consider 3 as initialization constant and different language may take different time for initialization.So other function remains f(n)=3n.
- We can ignore constant multiplier as different programming language may compile the code differently. For example array look up may take different number of instructions in different languages. So what we are left with is f(n)=n
How will you compare algorithms?
You can compare algorithms by its rate of growth with input size n.
Lets take a example.For solving same problem, you have two functions:
f(n) =4n^2 +2n+4 and g(n) =4n+4
For f(n) =4n^2+2n+4
so here
f(1)=4+2+4
f(2)=16+4+4
f(3)=36+6+4
f(4)=64+8+4
As you can see here contribution of n^2 increasing with increasing value of n.So for very large value of n,contribution of n^2 will be 99% of value on f(n).So here we can ignore low order terms as they are relatively insignificant as described above.In this f(n),we can ignore 2n and 4.so
n^2+2n+4 ——–>n^2. So here n^2 is highest rate of growth.
For g(n) =4n+4
so here
g(1)=4+4
g(2)=8+4
g(3)=12+4
g(4)=16+4
As you can see here contribution of n increasing with increasing value of n.So for very large value of n,contribution of n will be 99% of value on g(n).So here we can ignore low order terms as they are relatively insignificant.In this g(n),we can ignore 4 and also 4 as constant multiplier as seen above so
4n+4 ——–>n. So here n is highest rate of growth.
Point to be noted :
We are dropping all the terms which are growing slowly and keep one which grows fastest.
Lets take one more example:
Assume we need to find the sum of elements of an array:
int sum = 0;
int [] array = {5,1,9,2,7,3,4,8,10,2}
for(int i = 0; i < n; i++) {
sum = sum +array[i];
}
return sum;
In above case, if number of elements in array is 10, then n would be 10, and time taken to return the sum would be some x time. For instance, if number of elements in array increases, then time taken to return the sum would increase accordingly because in above case the number of instructions executed increases as n increases.
Let plot a graph where x axis determines the value of n, and y axis determines the time (in microseconds) taken to complete the program:
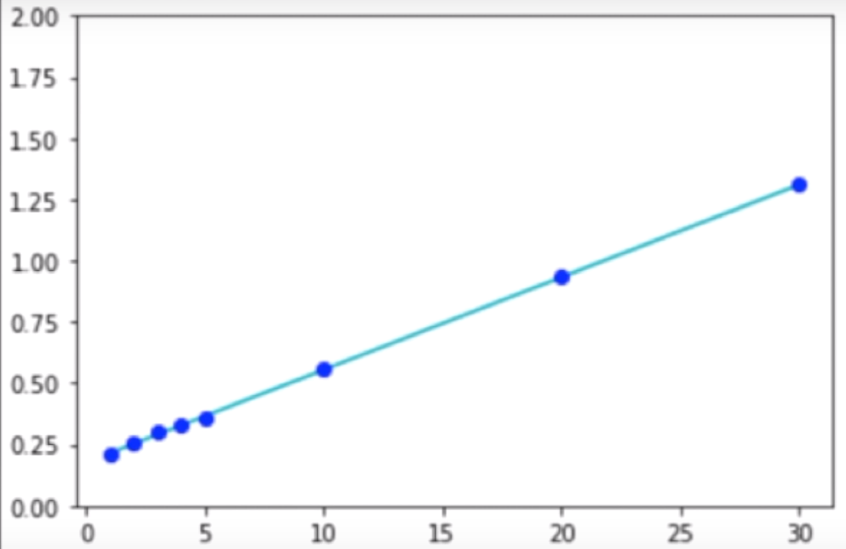
So, we can say as the size of n increases, the amount of time it takes to complete the function increases linearly.
So time complexity for above program would be liner time
Time complexity : Linear Time
So Time Complexity is basically a way of showing how the run-time of a function increases as the size of the input increases.
There are other types of time complexity for example:
- Linear Time —-> Already discussed.
- Constant Time —-> Here the time to execute the function remains constant even though we increase the value of n at a very high rate.
- Quadratic Time —-> Here the time to execute the functions increases in an exponential form, as we increase the value of n.
Linear Time – O(n)
Constant Time – O(1)
Quadratic Time – O(n^2)
We express above different types of time complexity, using a term Big O Notation.
To find the time complexity of any function, there are below 2 steps:
- Find the fastest growing term.
- Take out the coefficient.
Example1: Let take a function : T = an+b
First step: Here ‘an’ is the fastest growing term
Second step: Removing coefficient, so T = O(n) ==> Linear Time.
Example2: Let take a function : T = an^2+b
First step: Here ‘an^2’ is the fastest growing term
Second step: Removing coefficient, so T = O(n^2) ==> Quadratic Time.
Example3: Let take a function : T = a+b
Here, the program takes constant time, irrespective of value of n.
So, T = O(1) ==> Constant Time.
Let take another example, and this time the given input is 2d array:
int[][] array = {{1,2,3,4},
{5,6,7,8},
{9,1,2,3},
{4,5,6,7}}
void sum(int[][] a) {
int sum=0
for(int i=0; i<n;i++) { // for each row in 2d array
for(int j=0; j<n;j++) { // for each i in row
sum += a[i][j];
}
}
return sum;
}
So the Time complexity for above program will be:
T = O(1)+ n^2 * O(1) + O(1)T = c1 + n^2 * c2
T = O(n^2)
Asymptotic Notations:
- Asymptotic notations are used to measure the rate of growth of function, i.e the function is growing at what rate.
- The Asymptotic notations are used to calculate the running time complexity of a program.
- It analyze a program running time based on the input size.
- There are three types of Asymptotic notations used in Time Complexity, As shown below:
Ο (Big Oh) Notation:
Upper Bound
if f(n) <= c*g(n) for all n > n0
then f(n) = O(g(n))
It is used to describe the performance or complexity of a program.
Big O describes the worst-case scenario i.e the longest amount of time taken to execute the program.
f(n) = O(g(n)) means there are positive constants c and n0, such that 0 ≤ f(n) ≤ cg(n) for all n ≥ n0. The values of c and n0 must not be depend on n.
Example: Writing in a form of f(n)<=c*g(n) with f(n)=4n+3 and g(n)=5n
When n0 = 3, above condition get true, i.e 4n+3<=5n for n0=3 and c=5.
Ω (Omega) Notation:
Lower Bound
if f(n) >= c*g(n) for all n > n0
then f(n) = Ω(g(n))
Omega describes the best-case scenario i.e the best amount of time taken to execute the program
θ (theta) Notation:
Overall Bound
if c1*g(n) <= f(n) <= c2*g(n) for all n>n0, n>n1
then f(n) = θ(g(n))
Theta describes the both best case scenario and worst-case scenario of a program running time.
Common Asymptotic Notations:
| Constant | Ο(1) Example: Adding an element to the front of LinkedList. |
| Logarithmic | Ο(log n) Example: Finding an element in Sorted Array. Binary Search |
| Linear Logarithmic | Ο(n log n) Example: Merger Sort. |
| Linear | Ο(n) Example: Finding an element in Unsorted Array. |
| Quadratic | Ο(n2) Example: Shortest path between two nodes in Graph. |
| Cubic | Ο(n3) Example: Matrix multiplication. |
| Exponential | 2Ο(n) Example: Towers of Hanoi problem. |
| Factorial | O(n!) |
Some Important Formulas:

Lets understand the Big O Notation thoroughly by taking the java examples on common orders of growth like,
- O(1) – Constant
- O(log n) – Logarithmic
- O(n log n) – n log n
- O(n) – Linear
- O(n2) – Quadratic
- O(2n) – exponential
O(1): – Constant Time Algorithms
The O(1) is also called as constant time, it will always execute in the same time regardless of the input size. For example if the input array could be 1 item or 100 items, but this method required only one step.
Note:O(1) is best Time Complexity method.
public class sample {
static int y = 3;
static int z = 5;
public static void main(String[] args) {
int x = y + z; //O(1) complexity
System.out.println(x);
}
}
Output: 8
O(log n): – Logarithmic Time Algorithms
In O(log n) function the complexity increases as the size of input increases. Example: Binary Search.
for (int i = 1; i < n; i = i * 2){
System.out.println("Hey - I'm busy looking at: " + i);
}
Output:
Hey - I'm busy looking at: 1
Hey - I'm busy looking at: 2
Hey - I'm busy looking at: 4
O(n log n): – Linear Logarithmic Time Algorithms
The O(n log n) function fall between the linear and quadratic function ( i.e O(n) and Ο(n2). It is mainly used in sorting algorithm to get good Time complexity. For example Merge sort and quick sort.
for (int i = 1; i <= n; i++){
for(int j = 1; j < 8; j = j * 2) {
System.out.println("Hey - I'm busy looking at: " + i + " and " + j);
}
}
Output:
Hey - I'm busy looking at: 1 and 1
Hey - I'm busy looking at: 1 and 2
Hey - I'm busy looking at: 1 and 4
Hey - I'm busy looking at: 2 and 1
Hey - I'm busy looking at: 2 and 2
Hey - I'm busy looking at: 2 and 4
Hey - I'm busy looking at: 3 and 1
Hey - I'm busy looking at: 3 and 2
Hey - I'm busy looking at: 3 and 4
Hey - I'm busy looking at: 4 and 1
Hey - I'm busy looking at: 4 and 2
Hey - I'm busy looking at: 4 and 4
Hey - I'm busy looking at: 5 and 1
Hey - I'm busy looking at: 5 and 2
Hey - I'm busy looking at: 5 and 4
Hey - I'm busy looking at: 6 and 1
Hey - I'm busy looking at: 6 and 2
Hey - I'm busy looking at: 6 and 4
Hey - I'm busy looking at: 7 and 1
Hey - I'm busy looking at: 7 and 2
Hey - I'm busy looking at: 7 and 4
Hey - I'm busy looking at: 8 and 1
Hey - I'm busy looking at: 8 and 2
Hey - I'm busy looking at: 8 and 4
For example, if the n is 8, then this algorithm will run 8 * log(8) = 8 * 3 = 24 times. Whether we have strict inequality or not in the for loop is irrelevant for the sake of a Big O Notation.
O(n): – Linear Time Algorithms
The O(n) is also called as linear time, it is direct proportion to the number of inputs. For example if the array has 5 items, it will print 5 times.
Note: In O(n) the number of elements increases, the number of steps also increases.
public class sample {
public static void main(String[] args) {
int n = 5;
for (int i = 0; i < n; i++) // O(n) Complexity
System.out.println(i);
}
}
Output: 0 1 2 3 4
O(n2): – Polynomial Time Algorithms
The O(n2) is also called as quadratic time, it is directly proportional to the square of the input size. For example if the array has 2 items, it will print 4 times.
Note: In O(n2) as the number of steps increases exponential, number of elements also increases. It is the worst case Time Complexity method.
public class sample {
public static void main(String[] args) {
int n = 2;
for (int i = 0; i < n; i++) // O(n) Complexity
for (int j = 0; j < n; j++) //O(n) complexity
System.out.println(i + “, ”+j);
}
} // O(n)+O(n)=O(n^2) Complexity
Output: 0,0 0,1 1,0 1,1
For n = 2, we got 4 outputs.
Note, if we were to nest another for loop, this would become an O(n3) algorithm.
8.
O(2n): – Exponential Time Algorithms
- Algorithms with complexity O(2n) are called as Exponential Time Algorithms.
- These algorithms grow in proportion to some factor exponentiated by the input size.
- For example, O(2n) algorithms double with every additional input. So, if n = 2, these algorithms will run four times; if n = 3, they will run eight times (kind of like the opposite of logarithmic time algorithms).
- O(3n) algorithms triple with every additional input, O(kn) algorithms will get k times bigger with every additional input.
for (int i = 1; i <= Math.pow(2, n); i++){
System.out.println("Hey - I'm busy looking at: " + i);
}
Output:
Hey - I'm busy looking at: 1
Hey - I'm busy looking at: 2
Hey - I'm busy looking at: 3
.
.
.
Hey - I'm busy looking at: 254
Hey - I'm busy looking at: 255
Hey - I'm busy looking at: 256
This algorithm will run 28 = 256 times.
O(n!): – Factorial Time Algorithms
- This class of algorithms has a run time proportional to the factorial of the input size.
- A classic example of this is solving the traveling salesman problem using a brute-force approach to solve it.
for (int i = 1; i <= factorial(n); i++){
System.out.println("Hey - I'm busy looking at: " + i);
}
where factorial(n) simply calculates n!. If n is 8, this algorithm will run 8! = 40320 times.
Time Complexity analysis table for different Algorithms From best case to worst case
| Algorithm | Data structure | Best case | Average case | Worst case |
| Quick sort | Array | O(n log(n)) | O(n log(n)) | Ο(n2) |
| Merge sort | Array | O(n log(n)) | O(n log(n)) | O(n log(n)) |
| Heap sort | Array | O(n) | O(n log(n)) | O(n log(n)) |
| Smooth sort | Array | O(n) | O(n log(n)) | O(n log(n)) |
| Bubble sort | Array | O(n) | Ο(n2) | Ο(n2) |
| Insertion sort | Array | O(n) | Ο(n2) | Ο(n2) |
| Selection sort | Array | Ο(n2) | Ο(n2) | Ο(n2) |
Rules of thumb for calculating complexity of algorithm: Simple programs can be analyzed using counting number of loops or iterations.
Complexity of Consecutive statements: O(1).
int m=0; // executed in constant time c1
m=m+1; // executed in constant time c2
Complexity of a simple loop: O(n).
Time complexity of a loop can be determined by running time of statements inside loop multiplied by total number of iterations.
int m=0; // executed in constant time c1
// executed n times
for (int i = 0; i < n; i++) {
m=m+1; // executed in constant time c2
}
f(n)=c2*n+c1;
f(n) = O(n)
Complexity of a nested loop: O(n^2)
It is product of iterations of each loop.
int m=0; executed in constant time c1
// Outer loop will be executed n times
for (int i = 0; i < n; i++) {
// Inner loop will be executed n times
for(int j = 0; j < n; j++)
{
m=m+1; executed in constant time c2
}
}
f(n)=c2*n*n + c1
f(n) = O(n^2)
Complexity of If and else Block:
When you have if and else statement, then time complexity is calculated with whichever of them is larger.
int countOfEven = 0; //executed in constant time c1
int countOfOdd = 0; //executed in constant time c2
int k = 0; //executed in constant time c3
//loop will be executed n times
for (int i = 0; i < n; i++) {
if (i % 2 == 0) //executed in constant time c4
{
countOfEven++; //executed in constant time c5
k = k + 1; //executed in constant time c6
} else
countOfOdd++; //executed in constant time c7
}
f(n)=c1+c2+c3+(c4+c5+c6)*n
f(n) = O(n)
Logarithmic complexity:
Lets understand logarithmic complexity with the help of example.You might know about binary search.When you want to find a value in sorted array, we use binary search.
public int binarySearch(int[] sorted, int first, int last, int elementToBeSearched) {
int iteration = 0;
while (first < last) {
iteration++;
System.out.println("i" + iteration);
int mid = (first + last) / 2; // Compute mid point.
System.out.println(mid);
if (elementToBeSearched < sorted[mid]) {
last = mid; // repeat search in first half.
} else if (elementToBeSearched > sorted[mid]) {
first = mid + 1; // Repeat search in last half.
} else {
return mid; // Found it. return position
}
}
return -1; // Failed to find element
Now let’s assume our soreted array is:
int[] sortedArray={12,56,74,96,112,114,123,567};
and we want to search for 74 in above array. Below diagram will explain how binary search will work here.
When you observe closely, in each of the iteration you are cutting scope of array to the half. In every iteration, we are overriding value of first or last depending on soretedArray[mid].
So for
0th iteration : n
1th iteration: n/2
2nd iteration n/4
3rd iteration n/8.
Generalizing above equation:
For ith iteration : n/2i
So iteration will end , when we have 1 element left i.e. for any i, which will be our last iteration:
1=n/2i;
2i=n;
after taking log
i= log(n);
so it concludes that number of iteration requires to do binary search is log(n) so complexity of binary search is log(n)
It makes sense as in our example, we have n as 8 . It took 3 iterations(8->4->2->1) and 3 is log(8).
So If we are dividing input size by k in each iteration,then its complexity will be O(logk(n)) that is log(n) base k.
Lets take an example:
int m = 0;
// executed log(n) times
for (int i = 0; i < n; i = i * 2) {
m = m + 1;
}
Complexity of above code will be O(log(n)).
Exercise:
Lets do some exercise and find complexity of given code:
1.
int m = 0;
for (int i = 0; i < n; i++) {
m = m + 1;
}
Complexity will be O(n)
2.
int m = 0;
for (int i = 0; i < n; i++) {
m = m + 1;
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++)
m = m + 1;
}
}
Complexity will be :n+n*n —>O(n^2)
3.
int m = 0;
// outer loop executed n times
for (int i = 0; i < n; i++) {
// middle loop executed n/2 times
for (int j = n / 2; j < n; j++)
for (int k = 0; k * k < n; k++)
m = m + 1;
}
}
}
Complexity will be n*n/2*log(n)–> O(n^2log(n))
4.
int m = 0;
for (int i = n / 2; i < n; i++) {
for (int j = n / 2; j < n; j++)
for (int k = 0; k < n; k++)
m = m + 1;
}
Complexity will be n/2*n/2*n –> O(n^3)