Climbing Stairs

There are n stairs, a person standing at the bottom wants to reach the top. The person can climb either 1 stair or 2 stairs at a time. Count the number of ways, the person can reach the top.

Consider the example shown in diagram. The value of n is 3. There are 3 ways to reach the top.

Example 1:

Input: 2
Output: 2
Explanation: There are 2 ways to climb to the top.
1. 1 step + 1 step
2. 2 steps

Example 2:

Input: 3
Output: 3
Explanation: There are 3 ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step

Example 3:

Input: 4
Output: 5
Explanation: There are 5 ways to climb to the top.
1. 1 step + 1 step + 1 step + 1 step
2. 1 step + 1 step + 2 steps
3. 1 step + 2 steps + 1 step
4. 2 steps + 1 step + 1 step
5. 2 steps + 2 steps

Example 4:

Input: 5
Output: 8
Explanation: There are 8 ways to climb to the top.
1. 1 step + 1 step + 1 step + 1 step + 1 step 
2. 1 step + 1 step + 1 step + 2 steps
3. 1 step + 1 step + 2 steps + 1 step
4. 1 step + 2 steps + 1 step + 1 step 
5. 2 steps + 1 step + 1 step + 1 step 
6. 1 step + 2 steps + 2 steps
7. 2 steps + 2 steps + 1 step
8. 2 steps + 1 step + 2 steps   

Algorithm:

It’s always good to start off with some test cases. Let’s start with small cases and see if we can find some sort of pattern.

• N = 1, 1 way to climb: [1] ==> Same as fibonacci(2)
• N = 2, 2 ways to climb: [1, 1], [2] ==> Same as fibonacci(3)
• N = 3, 3 ways to climb: [1, 2], [1, 1, 1], [2, 1] ==> Same as fibonacci(4)
• N = 4, 5 ways to climb: [1, 1, 2], [2, 2], [1, 2, 1], [1, 1, 1, 1], [2, 1, 1] ==> Same as fibonacci(5)
• N = 5, 8 ways to climb: [1,1,1,1,1], [1,1,1,2], [1,1,2,1], [1,2,1,1], [2,1,1,1], [1,2,2], [2,1,2], [2,2,1] ==> Same as fibonacci(6)

Do you notice anything? When we look at N = 3, the number of ways to get to 3 steps is 3, and they’re based off N = 1 and N = 2. What’s the relationship?
The only ways to get to N = 3, is to first get to N = 1, and then go up by 2 steps, or get to N = 2 and go up by 1 step. So f(3) = f(2) + f(1).

Does this hold for N = 4? Yes, it does. Since we can only get to the 4th step by getting to the 3rd step and going up by one, or by getting to the 2nd step and going up by two. So f(4) = f(3) + f(2).

So the relationship looks like this: f(n) = f(n – 1) + f(n – 2), and f(1) = 1 and f(2) = 2. That’s just the Fibonacci sequence, except shifted by one because for N=1, the output is same as fib(2)=1, similarly for N=3. the output is same as fib(4) =3, similarly for N=5, the output is same as fib(6) =8.

Java Program:

public class StairCaseSolution {
	public static void main(String args[]) {
		int n = 5;
		System.out.println("Number of ways = " + countWays(n+1));
	}

	// Returns number of ways to reach n'th stair
	static int countWays(int n) {
		if (n <= 1)
			return n;
		return countWays(n - 1) + countWays(n - 2);
	}
}

Complexity:

Complexity Analysis

• Time complexity : O(2^n). Size of recursion tree will be 2^n.
• Space complexity : O(n). The depth of the recursion tree can go upto n.

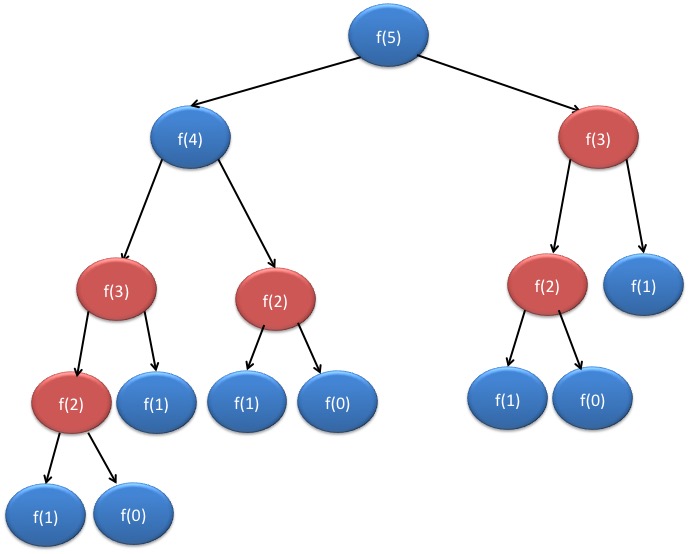
Let’s draw recursive tree for stair case with n=5.
Here two children of node will represent recursive call it makes.

If you notice here, we are calculating f(3) twice and f(2) thrice here, we can avoid duplication with the help of “Memoization”.

Java Program with Memoization:

import java.util.HashMap;
import java.util.Map;

public class StairCaseSolution {
	private static Map<Integer, Integer> memoMap = new HashMap<>();

	public static void main(String args[]) {
		int n = 5;
		System.out.println("Number of ways = " + countWays(n + 1));
	}

	// Returns number of ways to reach n'th stair
	static int countWays(int n) {
		if (n <= 1)
			return n;
		if (memoMap.containsKey(n)) {
			return memoMap.get(n);
		}
		int fibResult = countWays(n - 1) + countWays(n - 2);
		memoMap.put(n, fibResult);
		return fibResult;
	}
}

Complexity Analysis:

• Time complexity : O(n). Size of recursion tree can go upto n.
• Space complexity : O(n). The depth of recursion tree can go upto n.